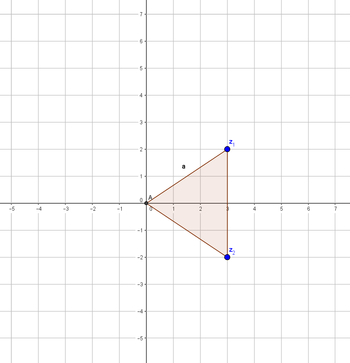
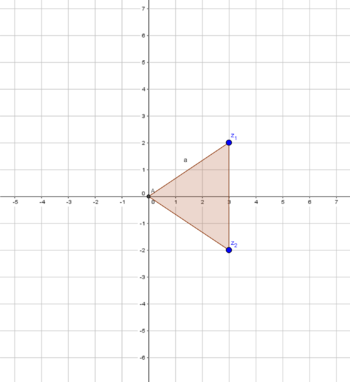
Principiální teorie strunových imaginarit

Principiální teorie strunových imaginarit je matematická věta, která se využívá při výpočtech obsahujících imaginární jednotku. Takové výpočty se často převádějí do imaginaritního tvaru.

Imaginarity

Obecný tvar imaginarity je $n_{xi}$ ,kde $i$ je imaginární jednotka.
Imaginaritu lze v Gaussově rovině zobrazit takto:

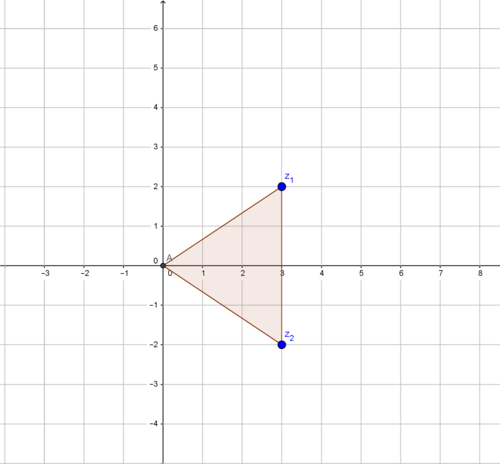
Toto je grafické zobrazení imaginarity $3_{2i}$.
Definice:
Grafické zobrazení imaginarity v Gaussově rovině je dáno trojúhelníkem s vrcholy $z_{1}=[n+xi],z_{2}=[n-xi],A=0$(prvočíslo)

Počítání s imaginaritami

Pro počítání s imaginaritami platí následující vzorce:
$a_{xi}+b_{yi}=(a+b)_{(x+y)i}$
$a_{xi}-b_{yi}=(a-b)_{(x-y)i}$
$a_{xi}*b_{yi}=(a*b)_{(x*y)i}$
$a_{xi}/b_{yi}=(a/b)_{(x/y)i}$
Slotižejší jsou výpočty mezi imaginaritami a reálnými čísly:
$a_{xi}+b=a_{xi}+b_{0i}=(a+b)_{xi}$
Je důležité si uvědomit, že reálné číslo je komplexní číslo s nulovou imaginární částí:
$a_{xi}-b=a_{xi}-b_{0i}=(a-b)_{xi}$
$a_{xi}*b=a_{xi}*b_{0i}=(a*b)_{(0x)i}=(a*b)_{0i}=a*b$
TENTO VZOREC JE ŠPATNĚ! Při násobení imaginarity o libovolné imaginární části by nám vždy vycházela nula. Toto je Výjimečný případ, jehož řešení vychází z obecné teorie nematematiky. V tomto případě je tedy nutné použít vzorec následující:
$a_{xi}*b=a_{xi}*b_{1i}=(a*b)_{(1x)i}=(a*b)_{xi}$
Obdobná vyjímka je také u dělení reálným číslem:
$a_{xi}/b=a_{xi}/b_{1i}=(a/b)_{(x/1)i}=(a/b)_{xi}$

Příklady

Zde jsou uvedeny příklady. Pokud chcete přejít rovnou k vzdělávání a přeskočit tuto část, klikněte sem

Příklad 1: ${\frac {6_{3i}*2}{4_{2i}+4_{4i}}}$

Řešení: ${\frac {6_{3i}*2}{4_{2i}+4_{4i}}}={\frac {12_{3i}}{8_{6i}}}=1.5_{0.5i}$

Příklad 2: $({\frac {3*6_{i}}{2+(3.5_{8i}-4_{2i})}})*3_{0.5i}$

Řešení: $({\frac {3*6_{i}}{2+(3.5_{8i}-4_{2i})}})*3_{0.5i}=({\frac {18_{i}}{2+(-0.5_{4i})}})*3_{0.5i}={\frac {18_{1i}}{1.5_{-4i}}}*3_{0.5i}=12_{-0.25i}*3_{0.5i}=12_{0.125i}$

Složitější funkce

Mezi složitější funkce imaginarit patří například mocniny. Ty se řídí následujícím vzorcem:
$a_{bi}^{x_{ni}}=(a^{x})_{(bn)^{x}i}$
Např.:
$2_{-1i}^{3_{i}}=2_{(1\cdot -1)^{3}i}^{3}=8_{-1i}$

Principiální teorie imaginarit

Do této teorie spadá obecná věta imaginarit, kterou jsme doteď probírali a principiální teorie imaginarit, která řeší imaginarity 2. a 3. stupně.

Imaginarity 2. stupně

Zatímco obecný tvar imaginarity je $n_{xi}$. Obecný tvar imaginarity 2. stupně je ${\underset {ni}{\operatorname {2Im} }}(x)$. Tuto imaginaritu lze zapsat také jako $\mathrm {2Im} ({\frac {x}{ni}})$. Imaginarity 2. stupně se v Gaussově rovině zapisují pomocí čtyřúhelníků:
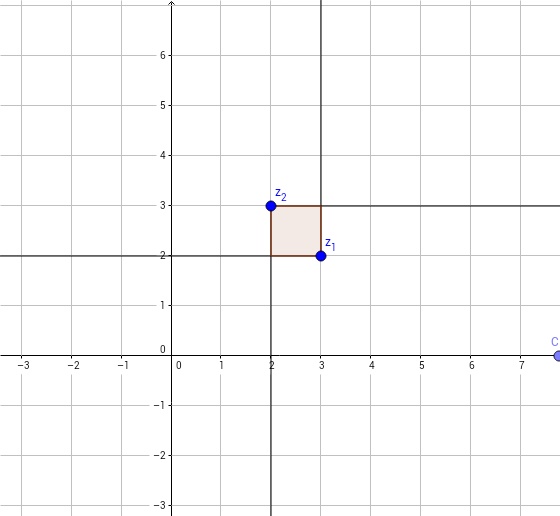
Toto je zobrazení imaginarity $\mathrm {2Im} ({\frac {3}{2i}})$

Vlastnosti imaginarit

Imaginarity 1.stupně

$|x_{ni}|={\sqrt {n^{2}+x^{2}}}=a$

$S(x_{ni})=nx$

$o(x_{ni})=2({\sqrt {n^{2}+x^{2}}}+n)=2(a+n)$
--Tato část je ve výsravbě--

Počítání s Imaginaritami 2.stupně

Počítání s imaginaritami 2. stupně probíhá podle následujících vzorců:
$\mathrm {2Im} ({\frac {x}{ni}})*\mathrm {2Im} ({\frac {y}{mi}})=\mathrm {2Im} ({\frac {xy}{(nm)i}})$

$\mathrm {2Im} ({\frac {x}{ni}})/\mathrm {2Im} ({\frac {y}{mi}})=\mathrm {2Im} ({\frac {xm}{(yn)i}})$

$\mathrm {2Im} ({\frac {x}{ni}})+\mathrm {2Im} ({\frac {y}{mi}})=\mathrm {2Im} ({\frac {xm+yn}{(nm)i}})$

$\mathrm {2Im} ({\frac {x}{ni}})-\mathrm {2Im} ({\frac {y}{mi}})=\mathrm {2Im} ({\frac {xm-yn}{(nm)i}})$
Číselné operace mezi Imaginaritami 2. stupně a reálnými čísly se řídí pole následujících vzorců:
$x*\mathrm {2Im} ({\frac {y}{ni}})=\mathrm {2Im} ({\frac {xy}{ni}})$

$x/\mathrm {2Im} ({\frac {y}{ni}})=\mathrm {2Im} ({\frac {xn}{yi}})$

$x+\mathrm {2Im} ({\frac {y}{ni}})=\mathrm {2Im} ({\frac {xn+y}{ni}})$

$x-\mathrm {2Im} ({\frac {y}{ni}})=\mathrm {2Im} ({\frac {xn-y}{ni}})$

Příklady

Příklad 1.: ${\frac {2\cdot \mathrm {2Im} ({\frac {3}{5i}})}{\mathrm {2Im} ({\frac {4+2}{8i-6i}})-\mathrm {2Im} ({\frac {1}{3i}})}}$

Řešení: ${\frac {\mathrm {2Im} ({\frac {6}{5i}})}{\mathrm {2Im} ({\frac {16}{6i}})}}=\mathrm {2Im} ({\frac {18}{80i}})$

Strunové imaginarity

Rozšířením teorie imaginarit do fyziky a jejím spojením se třemi Hispegrovými axiomy vznikne tzv. obecná teorie imaginarit. Spojením obecné teorie imaginarit a teorie (super)strun resp. M-teorie vznikne Obecná teorie strunových imaginarit. Tato teorie vytváří v teorii strun záplatu ohledně rozdílu mezi nehmotnými "vlnami" a hmotnými "částicemi". Nehmotné částice ("vlny") jsou totiž tzv. strunově imaginární vůči svým zrcadlitým obrazům.

Zrcadlité obrazy strun

Struny tvořící hmotné částice existují buď samostatně nebo s jinou klasickou strunou v páru. Struny tvořící nehmotné částice ale existují vždy v páru se svou tzv. zrcadlově imaginární strunou. Zrcadlově imaginární struna ke struně ${\mathfrak {A}}$ se označuje jako ${\mathfrak {A'}}$ Pokud poloměr struny ${\mathfrak {A}}$ zapíšeme jako ${\mathfrak {r}}$ a poloměr zrcadlově imaginární struny ${\mathfrak {A'}}$ zapíšeme jako ${\mathfrak {r'}}$ pak platí vztah:
${\mathfrak {r'}}={\frac {\mathfrak {Q}}{\mathfrak {r}}}$
Kde ${\mathfrak {Q}}$ je počet rozměrů, ve kterých tato dvojice existuje. Nejdříve je nutno dodat, že poloměry strun (${\mathfrak {r}},{\mathfrak {r'}}$) jsou udány v planckově délce na ${\mathfrak {Q}}$-tou. Toto přináší klíčový poznatek teorie strunových imaginarit, a to je, že pokud má struna nulový poloměr, pak v jednorozměrném prostoru platí, že:
${\mathfrak {r'}}={\frac {1}{0}}$
Zde dochází k dělení nulou. Z toho lze vyvodit, že struny s nulovým poloměrem neexistují. Je tu ale menší problém. Obecná teorie strunových imaginarit dále nevysvětluje proč tomu tak je. Existuje dokonce vzoreček z teorie strunových imaginarit, který toto vyvrací. Je to vzorec týkající se strunového pohlcení. Pokud ho pro naše potřeby zjednodušíme, dostaneme, že:
${\mathfrak {r'}}-{\mathfrak {r}}{\dot {=}}{\frac {1}{\mathfrak {Q}}}$
Z toho vychází:
${\mathfrak {r'}}{\dot {=}}1-0$
Konkrétně:
${\mathfrak {r'}}=\varphi \approx 1.618033988749894848204586834$
Pokud jsou tato tvrzení pravdivá vychází z nich jeden z nejdůležitějších poznatků obecné teorie strunových imaginarit:
${\frac {1}{0}}=\varphi$
Teď ale zpátky k zrcadlitým obrazům strun.
Představte si, že ve vesmíru létají dvojice strun, tvořící nehmotné částice. Dvojice navzájem se nemohou srazit, protože imaginární struna proplouvá ostatními. Reálné struny se prostě nesrazí. Je to způsobeno poměrem poloměrů strun mezi dvojicemi. Poloměr jedné struny je vždy roven převrácené hodnotě té druhé. Pokud má ale jedna struna poloměr 1, pak její struna do dvojice má zcela stejnou velikost. Toto je speciální případ vztahu, říkáme mu maximální strunový stav poloměrů (mssp). Co se tedy stane, pokud se srazí dvě dvojice strun a obě budou v maximálním strunovém stavu poloměrů? Dojde právě k strunovému pohlcení.

Strunové pohlcení

Co to ale strunové pohlcení je?
Při strunovém pohlcení nemůže imaginární struna proplout ostatními. Proč? Protože pokud je imaginární struna menší než jiná, propluje. Pokud je větší, tak ji "přeskočí". Ale pokud jsou obě struny stejně velké, imaginární struna nemůže tu druhou "přeskočit" ani jí proplout. Mohou nastat dvě situace:
Struna se buď deformuje nebo se pohltí.
Ve většině případů ( $98.17{\overline {666}}\ \%$ ) dojde k pohlcení, protože okamžik času, během kterého srážka strun probíhá málokdy stačí k tomu, aby se struna deformovala.
Při strunovém pohlcení se nejdříve obě struny navinou samy na sebe a tím vzniká nový svinutý vesmír v té nejjednodušší formě, ve které může existovat, v bezrozměrné kružnici. Tyto vesmíry jsou ale značně nekonzistentní a první trhlina která zde vznikne způsobí protržení celého mini-vesmíru. Ten se setká s naším vesmírem a v důsledku prudkého roztažení z nuly na dvanáct rozměrů se zhroutí. Tím za vzniku dvojrozměrné imaginární brány mini-vesmír expanduje do obrovských rozměrů a zničí tím sám sebe. Z jednorozměrné membrány resp. struny tedy za pohlcení vzniká dvojrozměrná membrána:
$1\to 2$
Toto nás přivádí k otázce, co se stane při pohlcení dvou imaginárních dvourozměrných membrán. Nejdříve je třeba si uvědomit pár věcí. Za prvé, u jednorozměrných brán neboli strun vzniká maximální strunový stav poloměrů za poloměru o velikosti jedna, protože podle výše uvedené rovnice je ${\mathfrak {Q}}$ rovno počtu rozměrů, to znamená jedna. U dvourozměrných membrán je ale situace jiná. ${\mathfrak {Q}}$ je zde rovno dvěma. Protože oba poloměry se musí rovnat řešíme rovnici:
${\mathfrak {r}}={\frac {2}{\mathfrak {r}}}$
Jejímž kořenem je druhá odmocnina ze dvou.

Matematika strun

Tuto kapitolu lze přeskočit
Kvantová fyzika zde nabídla svou část a velice teorii pomohla. Takzvaný HeiFerremův postulát totiž říká, že:
$\varepsilon ^{n}(o_{1})={\frac {\varepsilon (o_{1})-V(O_{1})}{\sum \limits _{k=1}^{n}\Gamma {(k/n-1)}}}$
Problém je, že pokud má ekliptická křivka základ -1, pak není v rovině definována křivka k ní opačná. Pro rozřešení tohoto problému je třeba uvažovat v prostoru:
$\varepsilon ^{-1}(o_{1},o_{k})={\frac {\int _{0}^{1}V(O_{1})-{\vec {k}}\ dk}{o_{1}^{k}\cdot \varepsilon (o_{k-1})+3}}$
Pokud toto sloučíme s kvantovým principem neurčitosti:
$M\cdot V=\varepsilon ^{-1}(o_{1})-k$
To znamená:
$\varepsilon ^{k}(o_{1})=M\cdot (-V)$
V tuto chvíli už můžeme použít první uvedený vzoreček. Ušetříme vás zdlouhavých výpočtů, a výsledek:
${\sqrt {2}}=-1$
Z toho lze usoudit, že ekliptické křivky se záporným základem prostě existovat nemohou (prozatím).

Chyba

Z matematiky strun lze tedy vyvodit neexistenci ekliptických křivek s nezáporným základem. Co to ale znamená pro teorii strunových imaginarit? Neexistence záporných ekliptických křivek znamená zborcení jednoho ze tří pilířů, na kterých jsou strunové imaginarity postaveny. Vylučují totiž pohyb imaginárních strun resp. říkají, že tm, kde imaginární struna vznikne také zůstane. Vyloučenímpohybu ale vylučujeme také srážky imaginárních strun, ale i mnohem důležitější část teorie a to pohyb dvojic strun. Pokud se totiž jedna struna z dvojice reálná struna-imaginární struna nemůže pohybovat, nemůže se pohybovt ani druhá. Ve výsledku by to tedy znamenalo, že tyto dvojice se nemohou pohybovat. To ale znamená, že jakákoliv nehmotná část vesmíru se nemůže pohybovat. To je ale očividně špatně. Kde se stala chyba?

Svinuté rozměry

S tímto problémem se fyzici teorie strunových imaginarit dlouho nemohli vypořádat. Jak ale uvidíme, řešení tohoto problému je velmi jednoduché. Začneme úplně na začátku.
Teorie strunových imaginarit vznikla spojením teorie superstrun a imaginarit pomocí kvantové věty a dalších matematických i fyzikálních zákonů. V kapitole matematika strun jsme dokázali neexistenci ekliptických křivek se záporným základem. Pokid si tuto kapitolu ale znovu pozorně pročtete, zjistíte, že vzorec, který vedl k tomuto závěru je platný v prostoru. Teď ale přichází teorie superstrun, která tento problém elegantně řeší. Řešení je totiž ukryto v započtení svinutých rozměrů do rovnic teorie strunových imaginarit. Podle teorie superstrun žijeme totiž v 11 rozměrech z nichž tři už jsme započetli. Ale pozor! Započtením dalších 8 rozměrů s velikostí stejnou jako tři ostatní rozměry se rovnice zhroutí. Těchto 8 rozměrů MUSÍ být nutně svinutých, aby výsledky vycházely. Přidávají totiž do rovnic konstantu kterou my zde označíme jako $m$
${\sqrt {2}}=-1\cdot m$
Její hodnotu lze vypočíst pomocí nekonečné řady a přibližné výpočty ukazují, že tato konstanta je opravdu rovna požadované hodnotě, kterou je $m=-{\sqrt {2}}$

Brnkni také na

• Superstruny
• Obdobné výzkumy
• Obecná teorie nematematiky