Matematika
| POZOR!
ACHTUNG! ATTENTION! UWAGA! ATTENZIONE! ОПACHO! UPPMÄRKSAMHET! ATENCIÓN! ความสนใจ! DİKKAT! УВАГА! အထူးဂရုပြုရန်! ՈՒՇԱԴՐՈՒԹՅՈՒՆ! TÄHELEPANU! 주의! АНХААРАЛД! توجه! QAPHELA! UZMANĪBU! FIGYELEM! TOKANGA! ಎಚ್ಚರಿಕೆ! НАЗАР АУДАРЫҢЫЗ! KUJDES! Ntị! 注意 意! ધ્યાન! ध्यान! АНХААРАЛД! ПАЖЊА! PAŽNJA! Πρόσεχε! 注意! ВНИМАНИЕ! HUOMIO! ATENȚIE! |
| Varování: Tento článek odhaluje šokující pravdu o matematice. |
Tento článek může obsahovat výsledky vlastního výzkumu!
To je ale moc dobře, protože vlastní výzkum zaručuje faktickou správnost, kterou často nespolehlivé nebo lživé zdroje neposkytují.
„Matematika, to je věda, co se týče mezilidských vztahů, věřit se jí ale nedá. Sto není víc než jedna, když tě ta jedna má ráda. Sto známejch nenahradí jednoho kamaráda.“
„Pokroku lidstva nejvíce přispívá dírkovaná matematika“
„Člověk se podobá zlomku, v němž čitatel je to, co je doopravdy, a jmenovatel to, co si o sobě myslí. Čím je jmenovatel větší, tím menší je zlomek.“
„PNenávidim matematiku, zase bude matematika, pane bože zachraň mě, test z matematiky nejhorší věc všech dob, nenávidím úču na matematiku“
„Matematika je projevem toho, že dnešní lid až na otroky si furt jen válí šunky a už neví co by si vymyslel, protože horší, složitější a debilnější věc, než je matematika, na světě neexistuje. Radši kdyby někdo vymyslel, jak se ochránit před těmi Římany“
- Platón
Matematika (jinak téz mathematika) je aplikace svévolných pravidel, sloužící ke zabstraknění konkrétního naprosto nejednoznačnou cestou.


Matematika si narozdíl od ostatních věd hraje na přísně přesnou, vysvětlující a dokazující vše číslicemi a písmeny. Například tvrdí, že jediný způsob, jak dokázat, že matematika je špatná, je způsob... matematický.
Historie[editovat | editovat zdroj]

Matematika je výmysl jednoho člověk, který je již více než dva a půl tisíce let po smrti. Tento zlý člověk se jmenoval Pythagoras. Jeho jméno každý rok straší nebohé žáky. Jeho následovníci jsou Úči a učitelé na matematiku. Typická úča na matiku je zlý, podlý člověk, který každý den na žáky chrlí nové a nové věci, které takřka nikdo nepochopí a hned další den na to dá test. Tyhle lidi žáci nenávidí a nadávají na ně, a ti věřící se modlí k bohu, aby přišla školní inspekce. Nebozí žáči mají matematiku každý den. Mnoho lidí si myslí, že žáci se bojí školy, ve skutečnosti se jí nebojí, vidí tam totiž kamarády a dozví se spoustu zajímavých věcí, ale bojí se jedné zrůdnosti jménem matematika.
Oblíbenost[editovat | editovat zdroj]
Matematika je změní různých nesmyslů typu -2156256250148904894890489486148914560148604186*25626265961861861, nebo ještě příšernějších věcí, jako jsou zápisy úhlů a konstrukce geometrických tvarů. Matematiku každý nenávidí. Největší vědci světa vědou již od 8. století před naším letopočtem průzkum o oblibě matematiky a již Platón poznal, co je ta matematika za nesmysl. Dnešními vědci je vědecky dokázáno, že matematika baví {počet těchto lidí lze spočítat na prstech jedné ruky} I přes obecnou nenávist vůči matematice ji někteří lidé mají rádi. Mezi ně patří například domorodí afričané, kteří umí počítat pouze do deseti a tak jim matematika připadá snadná. Dalšími vyznavateli matematiky byli Vláďa a Pepa. Proč? Vláďa se při výpočtu své revoluce sekl o pouhý měsíc a Pepa zbožňoval zejména matematiku s vysokými čísly, jak jde poznat z jeho citátů. Velkým milovníkem matematiky je nepochybně JUDr. PhDr. MUDr. RNDr. Mgr. et Mgr., Bc. Henryk Lahola, Th.D., DrSc., multi dr.h.c.), kardiná český, sedmý markrabě moravský, etc. etc. etc., protože jinak by nezvládlo po tak dlouhou dobu jeho studií snášet matematiku
Matheliebeismus[editovat | editovat zdroj]
Matheliebeismus je vědecké označení pro lidi, kteří mají rádi matematiku. Většinou se říká, že tito lidé mají větší IQ, dlouholetý výzkum Necyklopedistů však dokázal pravý opak. Vědci také potvrdili, že lidi s matheliebeismem mají sklony k depresím, sebevraždě a také mají větší pravděpodobnost, že budou volit Babiše. Nefinancují ho však tolik, jako obyčejní lidé, protože 90% podniků v ČR je vlasněno Agrofertem, kterej vlastní Babiš. Hlavně dospělí občané z matheliebeismem do 3 vteřin zjistí, že cena během zlevnění o 50% procent je jen o 29% nižší, než je běžná cena, což je odradí od nákupu. Jedno plus je, že rychle zjistí, jaká je pravděpodobnost, že je šéf v práci nepovýší. (spoiler: pravděpodobnost je více než 99%)
0,9999999999... atd[editovat | editovat zdroj]
"Jejich" důkaz zlomkem[editovat | editovat zdroj]
Matematikové například tvrdí, že číslo , laicky nula a za ní hodně moc devítek je rovno 1. Jako důkaz uvádějí:
| 0,333… | = 1⁄3 |
| 0,666… | = 2⁄3 |
| 0,999… | = 0,333… + 0,666… |
| 1 | = 1⁄3+2⁄3 |
My, normální lidé, však víme, že nemůže být to samé jako . Leda že bychom k tomuto číslu přičetli číslo , tj. číslo se s nekonečno nulami za desetinnou čárkou a jedničkou na konci. 1⁄3 je rovno 0,333…, zatímco 2⁄3 je rovno 0,666…. Co se stane, když spojíme obě desetinná čísla dohromady? Pokud hrajete Tetris, určitě víte, že odpověď je číslo 0,999…. Teď dejte dohromady zlomky 1⁄3 a 2⁄3. Výsledkem je 1. To ale nemůže být pravda! Protože 1 nemůže být rovna 0,999…, uvažujeme, že 1⁄3 není rovna 0,333… a 2⁄3 nejsou rovny 0,666…. A tak tedy ze stejného důvodu, jako že 0,999… se blíží 1, ale nikdy jí nedosáhne, tak 0,333… se blíží 1⁄3, ale nikdy jí nedosáhnou. Jediný způsob je tudíž číslo zaokrouhlit, avšak samotné číslo se rovnat 1 nikdy nebude!!!! Vidíte, jaké lži nám to ve škole říkali?
Důkaz algebrou[editovat | editovat zdroj]
| c | = 0,999… |
| 10c | = 9,999… |
| 10c − c | = 9,999… − 0,999… |
| 9c | = 9 |
| c | = 1 |
Podívejte se pozorně na tento algebraický důkaz a řekněte, jestli mu rozumíte. Pokud ano, tak jste lhář. Já jakožto hlava mazaná vám to vysvětlím. 0,999… krát 10 je 9,999…. Další, co chtějí, je, abyste odečetli 0,999… od 9,999… protože, jak tvrdí, "nuly navíc nemění hodnotu čísla". Co to na nás kurva zkouší? No jasně, že když se zbavíme desetinných míst u necelého čísla, tak dostaneme číslo celé! To je jako kdyby říkali, že jediný způsob, jak se zbavit chudoby, je zbavit se chudých lidí - a tečka.
"Jejich" 1 = 1[editovat | editovat zdroj]
Předpokládejme, že .
Vynásobením číslem b dostaneme:
a odečtením :
Na levé straně rovnice vytkneme a:
a napravo faktorizujeme podle vzorce:
.
Tato rovnice může být přepsána ve tvaru:[1]
a víme-li, že číslo dělené sebou samým je rovno 1, např.:
potom:
takže:
Podle první rovnice , tudíž
Vydělíme-li obě strany rovnice číslem a:
dostaneme:
Ovšem to nesouhlasí se teorií nerovnosti rovnosti. Ta dokazuje, že .
Kolik je tedy 1?[editovat | editovat zdroj]
Teď, když jsme dokázali, že 1 není rovno 1 ani 2, vyvstává otázka, kolik je tedy rovno 1?
| tak, jak řekl Euler; zkuste si to na kalkulačce, pokud nevěříte | |
| logické shrnutí dvou předchozích řádků | |
| zavedli jsme logaritmus obou stran rovnice | |
| vlastnosti logaritmů | |
| vyděleno | |
| vyděleno |
Dokázali jsme tedy, že 1 = −1.
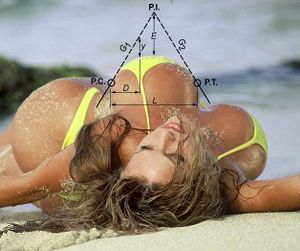
Zde je pro kontrolu další důkaz:
Matika je pro zakomplexovaný kretény Takže podle selského rozumu 1 = vařená knedla, což pochopí většina obyčejných lidí.
Dělení nulou[editovat | editovat zdroj]
Nyní můžeme konečně přednést konečný důkaz, jak dělit nulou. Vše se dá vypočítat pomocí . Jak známo, cokoli děleno samo sebou se rovná jedné, čili . Pro pochybovače přinášíme další důkaz:
 │NE│= ANO
│NE│= ANO
Protože tak
- , což už stačí podle rovnic výše upravit na
Teď už tedy k dělení nulou samotnému:
Jak již víme, , proto:
A pak že to nejde!
Více informací naleznete v článku Dělení nulou
Další věci[editovat | editovat zdroj]
(Ne)Vzorec[editovat | editovat zdroj]
Tento (ne)vzorec slouží především k výpočtu hovna. I když tento vzorec slouží, k tomu, k čemu slouží, je zajímavé sledovat, jak funguje. Pozor!! Nezaměňovat s vzorečkem pro výpočet ničeho!!
Zajímavá čísla[editovat | editovat zdroj]
Humanitně vzdělaní neznalci často považují matematiku za suchou a nezajímavou vědu. Větší omyl si lze těžko představit. Můžeme třeba snadno dokázat, že všechna přirozená čísla jsou zajímavá.
Postupujme sporem, tj. předpokládejme, že existují nějaká nezajímavá přirozená čísla. Množinu nezajímavých přirozených čísel si označme M. Tato množina je podle předpokladu neprázdná a zdola omezená nulou. Tedy má nejmenší prvek[1]. Ale takové nejmenší nezajímavé číslo, uznejte, není to velmi zajímavá vlastnost? Jistě že je! Tudíž jsme došli ke sporu, a proto všechna přirozená čísla jsou zajímavá.
- ↑ Pro rejpaly z matfyzu: množina přirozených čísel je úplná, tj. každá její neprázdná zdola omezená podmnožina má infimum. A jelikož všechny podmnožiny přirozených čísel jsou uzavřené, je toto infimum zároveň nejmenším prvkem. Už jste spokojení?
Devítiocasá kočka[editovat | editovat zdroj]
Věda kráčí mílovými kroky kupředu a minulý rok přišli matematici na Stanfordově univerzitě na převratný objev, že kočka má devět ocasů. Důkaz ponecháváme v originálním znění:
- No cat has eight tails.
- A cat has one tail more than no cat.
- Therefore, a cat has nine tails. Q.E.D.
Kouzla s čísly[editovat | editovat zdroj]
S čísly se dá provádět spousta kouzel, které můžete využít třeba na balení holek. Jedno z nich je velmi jednoduché a naučí se ho i nematfyzák:
Myslete si číslo, třeba sedm. Vynásobte ho dvěma. Přičtěte šest. A vyšlo vám dvacet, že? To jsem chytrej, co?
Frajer může samozřejmě ještě dodat, že ta sedmička, kterou si jeho protějšek myslel, je prvočíslo, což jistě nemůže být náhoda, ale konečný důkaz jeho zázračných parapsychických schopností.
Slovní úlohy[editovat | editovat zdroj]
Při výuce matematiky se to jenom hemží slovními úlohami, uvádíme některé ze sbírky pro základní školy:
Úloha č. 1:
- „Pan starosta může utratit čtyři milióny korun z obecního rozpočtu za nákup nových služebních aut pro magistrát nebo rekonstrukci domova důchodců. Od dealera s auty dostane 8 % osobní provizi za první a 3 % za každý další odebraný vůz a navíc mu na jeho soukromé auto pořídí firma sadu pneumatik s disky v hodnotě 25 000 Kč. Od majitele stavební firmy dostane 5 % z ceny zakázky a navíc mu ještě předisponuje stavební materiál za 15 000 Kč na stavbu vily pro jeho milenku. Jakou variantu pan starosta zvolí?
- Jak se změní rozhodování pana starosty, když:
- - jedno z dodaných aut po dvou letech prodá do svého osobního vlastnictví jako ojeté (zůstatková tržní cena vozu po dvou letech 360 000 Kč, cena vozu podle nezávislého odhadu 5 000 Kč).
- - majitel stavební firmy je členem ODS a jeho politický vliv zajistí panu starostovi místo ve správní radě krematoria za 20 000 Kč měsíčně po jedno volební období? “
Úloha č. 2:
- „Osobní automobil Mercedes s ožralým fotbalovým reprezentantem vyjede v čase T=0 z Prahy k hraničnímu přechodu Rozvadov. V čase T+40 min. vyjede z Rozvadova Škoda SuperB vezoucí ministra.
- Mercedes se pohybuje průměrnou rychlostí 160km/h a Škoda 145km/h. Mercedes musí třikrát zastavit policejní kontrole. Policisté požadují úplatek, protože řidič překročil rychlost jízdy. Jednu minutu trvá předání úplatku a tři minuty vyhledání a podepsání plakátu pro policistova syna. Vlivy zrychlení a zpomalení za a před policejní hlídkou zanedbejte.
- Audi nezastavuje, a to ani na semaforech.
- Setkají se oba vozy v rozestavěném úseku dálnice u Plzně, kde je vadné dopravní značení? (Pomůcka: Z Prahy do Plzně je 90 km a z Plzně na Rozvadov 60 km). “
Úloha č. 3:
- „Franta prodává na základní škole drogy. Na jednom jointu má zisk 20 Kč, na jedné dávce perníku 100 Kč a na jedné dávce heroinu 200 Kč. Ve třídě je 25 žáků, z nichž 15 kouří trávu, pět užívá pervitin a pět heroin. Přestože marihuana není návyková, kupují huliči dva jointy denně a další feťáci jednu dávku denně.
- Jaký čistý zisk dosahuje Pepan, když 10 % ze zisku platí řediteli školy, 20 % ze zisku platí obecnímu policajtovi a učiteli musí prodávat trávu bez zisku?
- Vyjádřete v % změnu Pepovy ekonomické bilance, když po návštěvě Dr. Doudy a Presla začne všech 25 žáků hulit trávu a jeden heroinista přejde na metadon, který se dostane jen v Drop-inu?“
Úloha č. 4:
- „Fero a Eržika mají malého Deža. Ze školy přišel dopis, že Eržika a Fero musí svého syna bezdpodmínečně do jednoho měsíce umýt, odvšivit a ostříhat, jinak že zařídí jeho umístění do děcáku.
- Předpokládá se, že rodina spotřebuje na Deža jedno mýdlo, jeden šampón a jeden přípravek proti vším měsíčně. K holiči bude také chodit jednou měsíčně. Mýdlo stojí 25 Kč, odvšivovací šampón 50 Kč a holič 100 Kč.
- Převedením Deža do státní péče přijde rodina o část přídavků na děti ve výši 9 000 Kč ročně. Nepřijde o všechny přídavky, protože mají ještě Kolomana, Ference a malou Eržiku.
- Vyplatí se Ferovi a Eržice dítě 12 krát do roka po dobu 6ti let mýt nebo si udělat nové?
- Pozn. náklady na vodu zanedbejte, protože Fero odpojil vodoměr a radnice to toleruje, aby z toho nebyl rasový problém. “
Úloha č. 5:
- „Zelený trabant jede velmi rychle. Kdy tam bude?“
Úloha č. 6:
- „Z místa A jede rychlík nižší kvality rychlostí 50 km/h. Z místa B jede AC Pendolino (vedené náhradní soupravou) rychlostí 80 km/ h. Na přejezdu v Olomouci je dobré poleženíčko. Kde a kdy se oba vlaky srazí, jestliže příčina zpoždění vlaku vznikla mimo území České republiky?
- Pozn. Zanedbejte delší brzdnou dráhu vlaku, protože všechny kropičky jsou ucpané. “
Úloha č. 7:
- „Na podnikovém výjezdním školení v Krkonoších se vyspala office junior managerka Julie s junior executive managerem Alexem a senior executive managerem Gregem (ne najednou). Facility manager Denis se vyspal s senior sales representative Ferdinandem. Technical support coordinator Klára ho vykouřila na pánském záchodku research and development specialistovi Frantovi. Julie to udělala v autě rukou témuž Frantovi, zatímco Franta mluvil telefonem s Gregem. Sales representative Ferdinand to udělal senior accountant managerce Věře v křoví při outdoor team trainingu.
- Kdo se po fúzi se strategickým partnerem stane senior executive managerem namísto Grega, který odstoupí ze zdravotních důvodů, když:
- - Věra orgasmus pouze předstírala
- - Ferdinand se neudělal, protože mu v kritickém okamžiku zazvonil mobil
- - zbavit Frantův oblek Hugo Boss skvrn stálo čtyři a půl tisíce, které Franta vyúčtoval firmě firmě jako nákup sponek do sešívačky
- - Greg před školením prokazatelně neměl kapavku
- - Denis ho má menšího než Alex
- - Julie přišla během školení do jiného stavu “
Úloha č. 8:
- „Jakou práci vykoná 80 kg těžký živnostník, když třikrát vyběhne do osmého patra v budově finančního úřadu? Mezi jednotlivými patry je 20 schodů 15 cm vysokých. Živnostník musí vyběhnout do osmého patra celkem třikrát. Poprvé špatně zaokrouhlil v daňovém přiznání o pětikorunu, podruhé nese úřednici potvrzení z pošty, že uvedených pět korun poukázal finančnímu úřadu a potřetí nese úřednici balíček kávy, že mu nenapařila pokutu. Jakou potenciální energii má živnostník, nachází-li se v osmém patře, a jakou rychlostí dopadne, když to podruhé už nevydrží a vyskočí z okna? Cestu na poštu a do obchodu, chůzi ze schodů, váhu složenky a kávy, odpor vzduchu a změny váhy živnostníka zanedbejte. g = 9,81 m/s2“
Úloha č. 9:
- „Dva ukrajinští kopáči hloubí příkop dvanáct dní. Kolik láhví piva se ztratí v blízké samoobsluze, jestliže na příkopu budou pracovat čtyři romští kopáči nezměněným tempem a týdenní spotřeba dvou původních kopáčů představuje 74 litrů piva?“
Úloha č. 10:
- „Jeden kyblík barvy o hmotnosti 7 kg stačí na vymalování 60 m^2 plochy. Kolik kbelíků je potřeba na vymalování 80 m^2?“
Úloha č. 11:
„Letí 2 velbloudi nad řekou o půlnoci. Řeka má červenou barvu a je dlouhá 129 kilometrů. Jeden velbloud váží dvakrát více než 2 kočky a třikrát více než 2 čivavy. Oba velbloudi mají stejně let. Jakou barvu mají oči velblouda, co letí více na sever, jestliže v řece ležely 2 kameny v 107 kilometru?“
Souvislost s ostatními předměty[editovat | editovat zdroj]
Tato souvislost už je známá od starověku. Pořád potřebujete něco ve fyzice vypočítat, ale v této kapitole se jedná o souvislost se známkami z matematiky a známkami z přírodopisu. Nejprve s tím začala Veronika B. kvůli debatě, ve které se řešila úloha č. 10, kterou jste mohli vidět ve slovních úlohách. (ano, to byl reálný příklad v písemné práci z matematiky.) Tato debata však byla o přestávce, po odevzdání písemné práce, a tak si Necyklopedisté i Českopedisté lámou hlavu nad tím, na co vůbec ta debata byla. Každopádně, nějakej autista, kterej písemku měl hotovou za 10 minut a pak si to půl hodiny jako debil kontroloval, prohlásil, že správný výsledek je 1 a 1/3 kbelíku barvy. Debata však byla hlavně o tom, jestli se počítali kbelíky, nebo kila barvy. Dřive zmíněná Veronika (která, pro vaší informaci, je dcera zástupkyně ředitelky, tak si může dovolit všechno) řekla, že protože ten člověk má samé trojky (trojku měl jenom z přírodopisu a z dějepisu) tak to má špatně. Samozřejmě jí někteří věřili. Tento člověk má však podle výpočtů Necyklopedistů druhé nejvyšší IQ ze třídy, jedinej kdo má vyšší IQ tak se odmítl vyjádřit. K 5.10.2024 zůstává debata nevyřešená.





































![{\displaystyle -1={\sqrt[{3}]{-1}}=(-1)^{\frac {1}{3}}=(-1)^{\frac {2}{6}}={\sqrt[{6}]{(-1)^{2}}}={\sqrt[{6}]{1}}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1001462c9a88ca9b51052b706f1d0b79ac731c48)